Вопросы для подготовки к зачету по теме: "Колебания и волны"
11. Механические колебания. Параметры колебательного движения. Уравнение гармонического колебания.
12. Математический и пружинный маятники. Периоды их колебаний. Превращение энергии при механических колебаниях.
13. Механические волны. Поперечные и продольные волны. Понятие фронта и длины волны.
38. Свободные электромагнитные колебания в колебательном контуре. Формула Томсона.
39. Электромагнитное поле и его распространение в пространстве в виде электромагнитных волн
40. Переменный ток, его получение и параметры. Уравнение переменного тока.
41. Действующие значения переменного тока и напряжения.
42. Активное, индуктивное и емкостное сопротивление в цепи переменного тока. Закон Ома для цепи переменного тока.
43. Устройство и принцип действия однофазного трансформатора.
Ответы.
Часть 1. Основные физические величины, единицы их измерения, формулы для нахождения.
Часть 2. Основные понятия.
Механические колебания – это движения, которые точно или приблизительно повторяются через одинаковые промежутки времени.
Смещение х – отклонение колеблющейся точки от положения равновесия. Единица измерения – 1 метр.
Амплитуда колебаний А – максимальноеотклонение колеблющейся точки от положения равновесия. Единица измерения – 1 метр.
Период колебаний T – минимальный интервал времени, за который происходит одно полное колебание, называется. Единица измерения – 1 секунда.
T=t/N
где t - время колебаний, N - количество колебаний, совершенных за это время.
По графику гармоническихколебаний можно определить период и амплитуду колебаний:
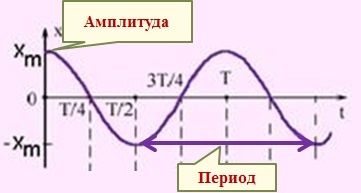
Частота колебаний ν – физическая величина, равная числу колебаний за единицу времени, показывает, сколько колебаний совершается за 1 с.Единица частоты – герц (Гц).
ν=N/t
Частота – величина, обратная периоду колебаний:
![]()
Циклическая частота ω – число колебаний за 2π секунды.
Частота колебаний ν связана с циклической частотой ω и периодом колебаний T соотношениями: ![]()
Фаза гармонического процесса – величина, стоящая под знаком синуса или косинуса в уравнении гармонических колебаний φ = ωt + φ0. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой.
Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением
x = xm cos (ωt + φ0)
x – смещение тела от положения равновесия
xm – амплитуда колебаний, то есть максимальное смещение от положения равновесия
ω – циклическая или круговая частота колебаний
t – время
Математический маятник - это тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела.
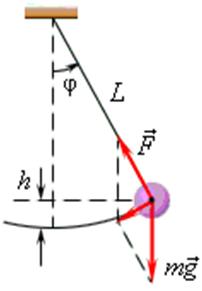
Период колебаний математического маятника:
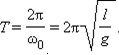
Период колебаний математического маятника зависит отдлины нити и от ускорения свободного падения той местности, где установлен маятник.
При гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при механических колебаниях остается неизменной.
Для математического маятника полная механическая энергия равна:
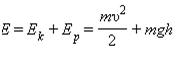
При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия равны нулю. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. В положении максимального отклонения полная энергия математического мятника равна потенциальной энергии тела, поднятого на высоту h:
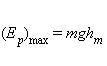
Здесь hm – максимальная высота подъема маятника в поле тяготения Земли.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна, значит, в этот момент оно обладает максимальной кинетической энергией. Тело находится на высоте нулевого уровня, значит, в этот момент оно обладает нулевой потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии.
При прохождении положения равновесия полная энергия равна кинетической энергии тела:
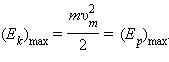
Тело проскакивает положение равновесия по закону инерции. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Здесь xm – максимальное значение отклонения маятника от положения равновесия, vm – максимальное значение его скорости.
Пружинный маятник - это груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно.
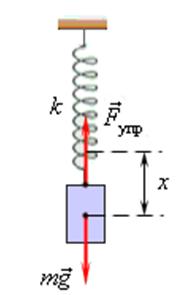
Период T гармонических колебаний груза на пружине равен
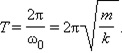
Период колебаний пружинного маятника зависит от массы груза и от жесткости пружины.
При гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при механических колебаниях остается неизменной.
Для пружинного маятника полная механическая энергия равна:
![]()
При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругих деформаций пружины, поэтому в положении максимального отклонения полная энергия мятника равна потенциальной энергии деформированной пружины:
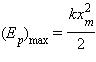
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна, значит, в этот момент оно обладает максимальной кинетической. Пружина при этом не деформирована, значит, в этот момент тело обладает нулевой потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии.
При прохождении положения равновесия полная энергия равна кинетической энергии груза:
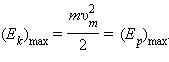
Тело проскакивает положение равновесия по закону инерции. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
