|
Инфофиз
Весь мир в твоих руках, всё будет так, как ты захочешь!
|
|
|---|
Инфофиз
Весь мир в твоих руках, всё будет так, как ты захочешь!
Физика для студентов
Принцип действия электродвигателя.
Электродвигатель – это просто устройство для эффективного преобразования электрической энергии в механическую.
В основе этого преобразования лежит магнетизм. В электродвигателях используются постоянные магниты и электромагниты, кроме того, используются магнитные свойства различных материалов, чтобы создавать эти удивительные устройства.
Существует несколько типов электродвигателей. Отметим два главных класса: AC и DC.
Электродвигатели класса AC (Alternating Current) требуют для работы источник переменного тока или напряжения (такой источник Вы можете найти в любой электрической розетке в доме).
Электродвигатели класса DC (Direct Current) требуют для работы источник постоянного тока или напряжения (такой источник Вы можете найти в любой батарейке).
Универсальные двигатели могут работать от источника любого типа.
Не только конструкция двигателей различна, различны способы контроля скорости и вращающего момента, хотя принцип преобразования энергии одинаков для всех типов.
Устройство и принцип работы простейшего электродвигателя.
В основе конструкции электрического двигателя лежит эффект, обнаруженный Майклом Фарадеем в 1821 году: что взаимодействие электрического тока и магнита может вызывать непрерывное вращение. Один из первых двигателей, нашедших практическое применение, был двигатель Бориса Семеновича Якоби (1801 –1874), приводивший в движение катер с 12 пассажирами на борту. Однако для широкого использования электродвигателя необходим был источник дешевой электроэнергии — электромагнитный генератор.
Принцип работы электродвигателя очень прост: вращение вызывается силами магнитного притяжения и отталкивания, действующими между полюсами подвижного электромагнита (ротора) и соответствующими полюсами внешнего магнитного поля, создаваемого неподвижным электромагнитом (или постоянным магнитом) — статором.
Вращающаяся часть электрической машины называется ротором (или якорем), а неподвижная - статором. В простом электродвигателе постоянного тока блок катушки служит ротором, а постоянный магнит - статором.
Сложность заключается в том, чтобы добиться непрерывного вращения двигателя. А для этого надо сделать так, чтобы полюс подвижного электромагнита, притянувшись к противоположному полюсу статора, автоматически менялся на противоположный — тогда ротор не замрет на месте, а повернется дальше — по инерции и под действием возникшего в этот момент отталкивания.
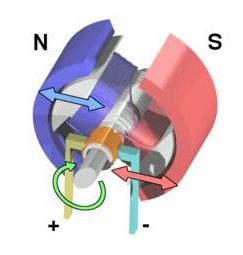
Для автоматического переключения полюсов ротора служит коллектор. Он представляет собой пару закрепленных на валу ротора пластин, к которым подключены обмотки ротора. Ток на эти пластины подается через токоснимающие контакты (щетки). При повороте ротора на 180° пластины меняются местами — это автоматически меняет направление тока и, следовательно, полюсы подвижного электромагнита. Так как одноименные полюсы взаимно отталкиваются, катушка продолжает вращаться, а ее полюсы притягиваются к соответствующим полюсам на другой стороне магнита.
Простейший электродвигатель
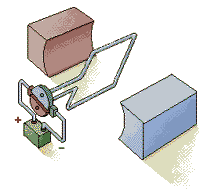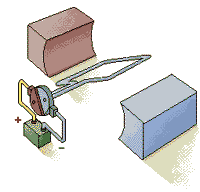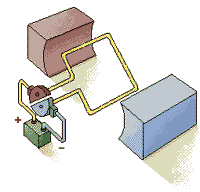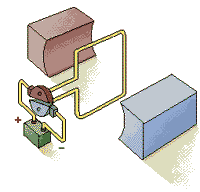
Простейший электродвигатель работает только на постоянном токе (от батарейки). Ток проходит по рамке, расположенной между полюсами постоянного магнита. Взаимодействие магнитных полей рамки с током и магнита заставляет рамку поворачиваться. После каждого полуоборота коллектор переключает контакты рамки, подходящие к батарейке, и поэтому рамка вращается.
В некоторых двигателях для создания магнитного поля вместо постоянного магнита служит электромагнит. Витки проволоки такого электромагнита называются обмоткой возбуждения.
Электродвигатели используются повсюду. Даже дома вы можете обнаружить огромное количество электродвигателей. Электродвигатели используются в часах, в вентиляторе микроволновой печи, в стиральной машине, в компьютерных вентиляторах, в кондиционере, в соковыжималке и т. д. и т. п. Ну а электродвигатели, применяемые в промышленности, можно перечислять бесконечно. Диапазон физических размеров – от размера со спичечную головку до размера локомотивного двигателя.
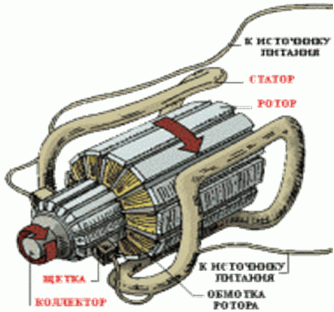
Показанный ниже промышленный электродвигатель работает и на постоянном, и на переменном токе. Его статор – это электромагнит, создающий магнитное поле. Обмотки двигателя поочередно подключаются через щетки к источнику питания. Одна за другой они поворачивают ротор на небольшой угол, и ротор непрерывно вращается.
Промышленный электродвигатель
Электроизмерительные приборы.
Электроизмерительные приборы - класс устройств, применяемых для измерения различных электрических величин.
Группа электромагнитных приборов является наиболее распространенной. Принцип их действия, использованный впервые еще Ф. Кольраушем в 1884 году, основан на перемещении подвижной железной части под влиянием магнитного потока, создаваемого катушкой, по которой пропускается ток. Практическое осуществление этого принципа отличается разнообразием.
Ориентирующее действие магнитного поля на контур с током используют в электроизмерительных приборах магнитоэлектрической системы – амперметрах, вольтметрах и др.
Устройство прибора магнитоэлектрической системы
Измерительный прибор магнитоэлектрической системы устроен следующим образом.
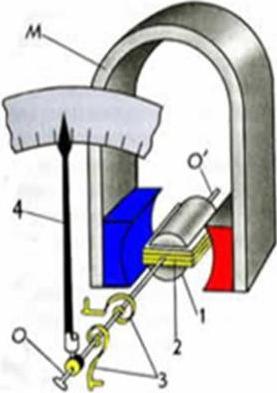
Берут лёгкую алюминиевую рамку 2 прямоугольной формы, наматывают на неё катушку из тонкого провода. Рамку крепят на двух полуосях О и О', к которым прикреплена также стрелка прибора 4. Ось удерживается двумя тонкими спиральными пружинами 3. Силы упругости пружин, возвращающие рамку к положению равновесия в отсутствие тока, подобраны такими, чтобы были пропорциональными углу отклонения стрелки от положения равновесия. Катушку помещают между полюсами постоянного магнита М с наконечниками формы полого цилиндра. Внутри катушки располагают цилиндр 1 из мягкого железа. Такая конструкция обеспечивает радиальное направление линий магнитной индукции в области нахождения витков катушки (см рисунок).
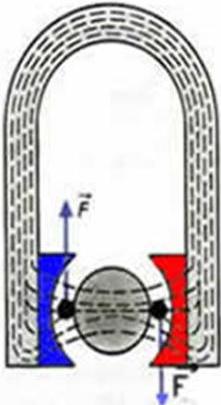
В результате при любом положении катушки силы, действующие на нее со стороны магнитного поля, максимальны и при неизменной силе тока постоянны. Векторы F и –F изображают силы, действующие на катушку со стороны магнитного поля и поворачивающие ее. Катушка с током поворачивается до тех пор, пока силы упругости со стороны пружины не уравновесят силы, действующие на рамку со стороны магнитного поля. Увеличивая силу тока в рамке в 2 раза, рамка повернётся на угол, вдвое больший. Это происходит потому, что Fm~I.
Силы, действующие на рамку с током прямо пропорциональны силе тока, то есть можно, проградуировав прибор, измерять силу тока в рамке.
Точно так же можно прибор настроить на измерение напряжения в цепи, если проградуировать шкалу в вольтах, причём сопротивление рамки с током должно быть выбрано очень большим по сравнению с сопротивлением участка цепи, на котором измеряем напряжение.
Дополнительные материалы.
1. Видео-ролик "Принцип работы электродвигателя"
2. Презентация "Электроизмерительные приборы" скачать с Яндекса
Медиа-материалы из Единой коллекции Цифровых Образовательных Ресурсов:
Рисунок "Вольтметр" 8_140
Рисунок-плакат "Электродвигатель" 8_224
Слайд-шоу "Работа электродвигателя" 8_225
Рисунок-плакат "Электроизмерительный прибор электродинамической системы" 8_227
Рисунок-плакат "Электроизмерительный прибор" 8_228
Слайд-шоу "Работа амперметра" 8_229
Слайд-шоу "Работа электроизмерительного прибора" 8_230
Взаимная связь электрических и магнитных полей была установлена выдающимся английским физиком М. Фарадеем в 1831 г. Он открыл явление электромагнитной индукции. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
Явление электромагнитной индукции заключается в возникновении электрического тока в замкнутом контуре при изменении магнитного потока, пронизывающего контур.
Магнитным потоком Φ через площадь S контура называют величину Ф = BScosα
где B – модуль вектора магнитной индукции, α – угол между вектором B и нормалью n к плоскости контура.
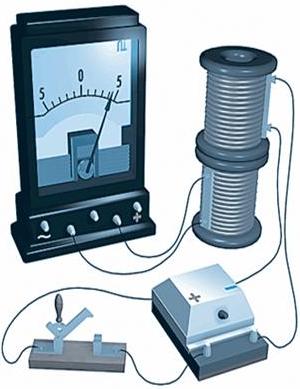
Явление электромагнитной индукции Фарадей исследовал с помощью двух изолированных друг от друга проволочных спиралей, намотанных на деревянную катушку. Одна спираль была присоединена к гальванической батарее, а другая — к гальванометру, регистрирующему слабые токи. В моменты замыкания и размыкания цепи первой спирали стрелка гальванометра в цепи второй спирали отклонялась.
Опыты Фарадея.
Опыты Фарадея по исследованию ЭМИ можно разделить на две серии:
1. возникновение индукционного тока при вдвигании и выдвигании магнита (катушки с током);
Объяснение опыта: При внесении магнита в катушку, соединенную с амперметром в цепи возникает индукционный ток. При удалении так же возникает индукционный ток, но другого направления. Видно, что индукционный ток зависит от направления движения магнита, и каким полюсом он вносится. Сила тока зависит от скорости движения магнита.
2. возникновение индукционного тока в одной катушке при изменении тока в другой катушке.
Объяснение опыта: электрический ток в катушке 2 возникает в моменты замыкания и размыкания ключа в цепи катушки 1. Видно, что направление тока зависит от того, замыкаюи или размыкают цепь катушки 1, т.е. от того, увеличивается (при замыкании цепи) или уменьшаетя (при размыкании цепи) магнитный поток. пронизывающий 1-ю катушку.
Проводя многочисленные опыты Фарадей установил, что в замкнутых проводящих контурах электрический ток возникает лишь в тех случаях, когда они находятся в переменном магнитном поле, независимо от того, каким способом достигается изменение потока индукции магнитного поля во времени.
Ток, возникающий при явлении электромагнитной индукции, называют индукционным.
Строго говоря, при движении контура в магнитном поле генерируется не определенный ток (который зависит от сопротивления), а определенная э. д. с.
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции Eинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Эта формула выражает закон Фарадея: э. д. с. индукции равна скорости изменения магнитного потока через поверхность, ограниченную контуром.
Знак минус в формуле отражает правило Ленца.
В 1833 году Ленц опытным путем доказал утверждение, которое называется правилом Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
При возрастании магнитного потока Ф>0, а εинд < 0, т.е. э. д. с. индукции вызывает ток такого направления, при котором его магнитное поле уменьшает магнитный поток через контур.
При уменьшении магнитного потока Ф<0, а εинд > 0, т.е. магнитное поле индукционного тока увеличивает убывающий магнитный поток через контур.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии: если магнитное поле через контур увеличивается, то ток в контуре направлен так, что его магнитное поле направлено против внешнего, а если внешнее магнитное поле через контур уменьшается, то ток направлен так, что его магнитное поле поддерживает это убывающее магнитное поле.
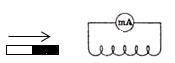
ЭДС индукции зависит от разных причин. Если вдвигать в катушку один раз сильный магнит, а в другой — слабый, то показания прибора в первом случае будут более высокими. Они будут более высокими и в том случае, когда магнит движется быстро. В каждом из проведённых в этой работе опыте направление индукционного тока определяется правилом Ленца. Порядок определения направления индукционного тока показан на рисунке.
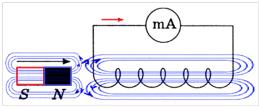
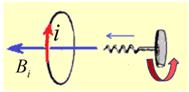
На рисунке синим цветом обозначены силовые линии магнитного поля постоянного магнита и линии магнитного поля индукционного тока. Силовые линии магнитного поля всегда направлены от N к S – от северного полюса к южному полюсу магнита.
По правилу Ленца индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока. Поэтому в катушке направление силовых линий магнитного поля противоположно силовым линиям постоянного магнита, ведь магнит движется в сторону катушки. Направление тока находим по правилу буравчика: если буравчик (с правой нарезкой) ввинчивать так, чтобы его поступательное движение совпало с направлением линий индукции в катушке, тогда направление вращения рукоятки буравчика совпадает с направлением индукционного тока.
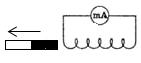
Поэтому ток через миллиамперметр течёт слева направо, как показано на рисунке красной стрелкой. В случае, когда магнит отодвигается от катушки, силовые линии магнитного поля индукционного тока будут совпадать по направлению с силовыми линиями постоянного магнита, и ток будет течь справа налево.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.
1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках.. Электродвижущая сила в цепи — это результат действия сторонних сил, т.е. сил неэлектрического происхождения. Сила Лоренца играет в этом случае роль сторонней силы, под действием которой происходит разделение зарядов, в результате чего на концах проводника появляется разность потенциалов.
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле В, перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью v по двум другим сторонам.
На свободные заряды на этом участке контура действует сила Лоренца. Составляющая силы Лоренца, действующая на свободный электрон, связанная с переносной скоростью v зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 3. Это она играет роль сторонней силы. Ее модуль равен FЛ = eυB
Э. д. с. индукции в проводнике характеризует работу по перемещению единичного положительного заряда вдоль проводника.
Работа силы FЛ на пути l равна A = FЛ · l = eυBl
По определению ЭДС
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для инд можно придать привычный вид. За времы Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный
Iинд = инд/R.
За время Δt на сопротивлении R выделится джоулево тепло
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера FA . Для случая, изображенного на рис. 3, модуль силы Ампера равен FA = IBl. Сила Ампера направлена навстречу движения проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
При движении проводника вправо свободные электроны, содержащиеся в нем, будут двигаться также вправо, т. е. возникает конвекционный ток. Направление этого тока обратно направлению движения электронов.
На каждый движущийся электрон со стороны магнитного поля действует сила Лоренца Fл. Заряд электрона — отрицательный. Поэтому сила Лоренца направлена вниз.
Под действием этой силы электроны будут двигаться вниз, поэтому в нижней части проводника l накапливаются отрицательные заряды, а в верхней — положительные. Образуется разность потенциалов φ1 - φ2, в проводнике возникает электрическое поле напряженностью Е, которое препятствует дальнейшему перемещению электронов.
В момент, когда сила Fэл = еЕ, действующая на заряды со стороны этого электрического поля, станет равной по модулю силе Fл = evBsinα, действующей на заряды со стороны магнитного поля, т.е. при еЕ = evBsinα или Е = vBsinα , заряды перестанут перемещаться.
Напряженность электрического поля Е в движущемся проводнике длиной l и разность потенциалов φ1 - φ2 связаны между собой соотношением
φ1 - φ2 = El
или
φ1 - φ2 = vBlsinα
Если такой проводник замкнуть, то по цепи пойдет ток. Таким образом, на концах проводника индуцируется э.д. с.
εинд = vBlsinα
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом (1861 г.).
Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Явление электромагнитной индукции лежит в основе действия электрических генераторов. Если равномерно вращать проволочную рамку в однородном магнитном поле, то возникает индуцированный ток, периодически изменяющий свое направление. Даже одиночная рамка, вращающаяся в однородном магнитном поле, представляет собой генератор переменного тока. Более сложные генераторы обычно являются улучшенными вариантами такого устройства.
Лабораторная работа № 9
Изучение явления электромагнитной индукции
Цель работы: изучить условия возникновения индукционного тока, ЭДС индукции.
Оборудование: катушка, два полосовых магнита, миллиамперметр.
Теория
Взаимная связь электрических и магнитных полей была установлена выдающимся английским физиком М. Фарадеем в 1831 г. Он открыл явление электромагнитной индукции.
Многочисленные опыты Фарадея показывают, что с помощью магнитного поля можно получить электрический ток в проводнике.
Явление электромагнитной индукции заключается в возникновении электрического тока в замкнутом контуре при изменении магнитного потока, пронизывающего контур.
Ток, возникающий при явлении электромагнитной индукции, называют индукционным.
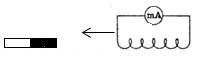
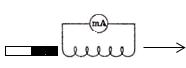
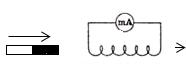
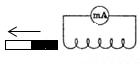
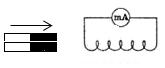
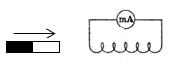
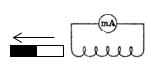
В электрической цепи (рисунок 1) возникает индукционный ток, если есть движение магнита относительно катушки, или наоборот. Направление индукционного тока зависит как от направления движения магнита, так и от расположения его полюсов. Индукционный ток отсутствует, если нет относительного перемещения катушки и магнита.
Рисунок 1.
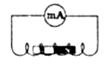
Строго говоря, при движении контура в магнитном поле генерируется не определенный ток , а определенная э. д. с.
Рисунок 2.
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции Eинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Эта формула выражает закон Фарадея: э. д. с. индукции равна скорости изменения магнитного потока через поверхность, ограниченную контуром.
Знак минус в формуле отражает правило Ленца.
В 1833 году Ленц опытным путем доказал утверждение, которое называется правилом Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
При возрастании магнитного потока Ф>0, а εинд < 0, т.е. э. д. с. индукции вызывает ток такого направления, при котором его магнитное поле уменьшает магнитный поток через контур.
При уменьшении магнитного потока Ф<0, а εинд > 0, т.е. магнитное поле индукционного тока увеличивает убывающий магнитный поток через контур.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии: если магнитное поле через контур увеличивается, то ток в контуре направлен так, что его магнитное поле направлено против внешнего, а если внешнее магнитное поле через контур уменьшается, то ток направлен так, что его магнитное поле поддерживает это убывающее магнитное поле.
ЭДС индукции зависит от разных причин. Если вдвигать в катушку один раз сильный магнит, а в другой — слабый, то показания прибора в первом случае будут более высокими. Они будут более высокими и в том случае, когда магнит движется быстро. В каждом из проведённых в этой работе опыте направление индукционного тока определяется правилом Ленца. Порядок определения направления индукционного тока показан на рисунке 2.
На рисунке синим цветом обозначены силовые линии магнитного поля постоянного магнита и линии магнитного поля индукционного тока. Силовые линии магнитного поля всегда направлены от N к S – от северного полюса к южному полюсу магнита.
По правилу Ленца индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока. Поэтому в катушке направление силовых линий магнитного поля противоположно силовым линиям постоянного магнита, ведь магнит движется в сторону катушки. Направление тока находим по правилу буравчика: если буравчик (с правой нарезкой) ввинчивать так, чтобы его поступательное движение совпало с направлением линий индукции в катушке, тогда направление вращения рукоятки буравчика совпадает с направлением индукционного тока.
Поэтому ток через миллиамперметр течёт слева направо, как показано на рисунке 1 красной стрелкой. В случае, когда магнит отодвигается от катушки, силовые линии магнитного поля индукционного тока будут совпадать по направлению с силовыми линиями постоянного магнита, и ток будет течь справа налево.
Ход работы.
Подготовьте для отчета таблицу и по мере проведения опытов заполните её.
|
№ п/п |
Действия с магнитом и катушкой |
Показания милли-амперметра, мА |
Направления отклонения стрелки миллиампер-метра (вправо, влево или не откланяется) |
Направление индукционного тока (по правилу Ленца) |
|
1 |
Быстро вставить магнит в катушку северным полюсом |
|
|
|
|
2 |
Оставить магнит в катушке неподвижным после опыта 1 |
|
|
|
|
3 |
Быстро вытащить магнит из катушки |
|
|
|
|
4 |
Быстро приблизить катушку к северному полюсу магнита |
|
|
|
|
5 |
Оставить катушку неподвижной после опыта 4 |
|
|
|
|
6 |
Быстро вытащить катушку от северного полюса магнита |
|
|
|
|
7 |
Медленно вставить в катушку магнит северным полюсом |
|
|
|
|
8 |
Медленно вытащить магнит из катушки |
|
|
|
|
9 |
Быстро вставить в катушку 2 магнита северными полюсами |
|
|
|
|
10 |
Быстро вставить магнит в катушку южным полюсом |
|
|
|
|
11 |
Быстро вытащить магнит из катушки после опыта 10 |
|
|
|
|
12 |
Быстро вставить в катушку 2 магнита южными полюсами |
|
|
|
Записать общий вывод по работе на основе проведённых наблюдений.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
- В чем заключается явление электромагнитной индукции?
- Какой ток называют индукционным?
- Сформулируйте закон электромагнитной индукции. Какой формулой он описывается?
- Как формулируется правило Ленца?
- Какова связь правила Ленца с законом сохранения энергии?
Презентация для демонстрации студентам (с решением): скачать с Яндекс-Диск
Видео Лабораторная работа «Изучение явления электромагнитной индукции»
Лабораторная работа.
Тема: Изучение зависимости периода колебаний нитяного маятника от длины нити.
Оборудование: штатив с перекладиной и муфтой, нить с петлями на концах, груз с крючком, линейка, электронный секундомер
Цель работы: состоит в экспериментальной проверке формулы, связывающей период колебаний маятника с длиной его подвеса.
Основные сведения
Рассмотрим колебания нитяного маятника, т.е. небольшого тела (например, шарика), подвешенного на нити, длина которой значительно превышает размеры самого тела. Если шарик отклонить от положения равновесия и отпустить, то он начнет колебаться. Сначала маятник движется с нарастающей скоростью вниз. В положении равновесия скорость шарика не равна нулю, и он по инерции движется вверх. По достижении наивысшего положения шарик снова начинает двигаться вниз. Это будут свободные колебания маятника.
Свободные колебания – это колебания, которые возникают в системе под действием внутренних сил, после того, как система была выведена из положения устойчивого равновесия.
Колебательное движение характеризуют амплитудой, периодом и частотой колебаний.
Амплитуда колебаний - это наибольшее смещение колеблющегося тела от положения равновесия. Обозначается А. Единица измерения - метр [1м].
Период колебаний - это время, за которое тело совершает одно полное колебание. Обозначается Т. Единица измерения - секунда [1с].
Частота колебаний - это число колебаний, совершаемых за единицу времени. Обозначается ν. Единица измерения - герц [1Гц].
Тело, подвешенное на невесомой нерастяжимой нити называют математическим маятником.
Период колебаний математического маятника определяется формулой: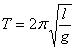 
(1), где l – длина подвеса, а g – ускорение свободного падения.
Период колебаний математического маятника зависит:
1) от длины нити. Период колебаний математического маятника пропорционален корню квадратному из длины нити 
. Т.е., например при уменьшении длины нити в 4 раза, период уменьшается в 2 раза; при уменьшении длины нити в 9 раз, период уменьшается в 3 раза.
2) от ускорения свободного падения той местности, где происходят колебания. Период колебаний математического маятника обратнопропорционален корню квадратному из ускорения свободного падения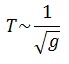 
.
Тело, подвешенное на пружине называют пружинным маятником.
Период колебаний пружинного маятника определяется формулой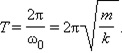 
, где m - масса тела, k - жесткость пружины.
Период колебаний пружинного маятника зависит:
1) от массы тела. Период колебаний пружинного маятника пропорционален корню квадратному из массы тела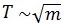 
.
2) от жесткости пружины. Период колебаний пружинного маятника обратнопропорционален корню квадратному из жесткости пружины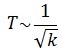
.
В работе мы исследуем колебания математического маятника. Из формулы 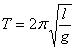следует, что период колебаний изменится вдвое при изменении длины подвеса в четыре раза.
Это следствие и проверяют в работе. Поочередно испытывают два маятника, длины подвесов которых отличаются в четыре раза. Каждый из маятников приводят в движение и измеряют время, за которое он совершит определённое количество колебаний. Чтобы уменьшить влияние побочных факторов, опыт с каждым маятником проводят несколько раз и находят среднее значение времени, затраченное маятником на совершение заданного числа колебаний. Затем вычисляют периоды маятников и находят их отношение.
Выполнение работы.
1. Подготовьте таблицу для записи результатов измерений и вычислений:
|
l, м |
№ опыта |
N |
t, с |
tср, с |
Т, с |
ν, Гц |
|
l1 = |
1 |
30 |
|
|
|
|
|
2 |
30 |
|
||||
|
3 |
30 |
|
||||
|
4 |
30 |
|
||||
|
l2 = |
1 |
30 |
|
|
|
|
|
2 |
30 |
|
||||
|
3 |
30 |
|
||||
|
4 |
30 |
|
2. Закрепите перекладину в муфте у верхнего края стержня штатива. Штатив разместите на столе так, чтобы конец перекладины выступал за край поверхности стола. Подвесьте к перекладине с помощью нити один груз из набора. Расстояние от точки повеса до центра груза должно быть 25-30 см.
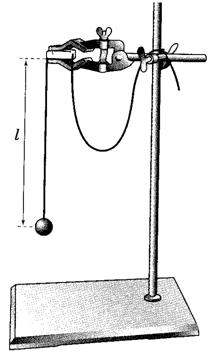
3. Подготовьте электронный секундомер к работе в ручном режиме.
4. Отклоните груз на 5-6 см от положения равновесия и замерьте время, за которое груз совершит 30 полных колебаний (при отклонении груза следите, чтобы угол отклонения не был велик).
5. Повторите измерение 3-4 раза и определите среднее время tср1=(t1+t2+t3+t4)/4
6. Вычислите период колебания груза с длиной подвеса 25-30 см по формуле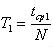 
.
7. Увеличьте длину подвеса в четыре раза.
8. Повторите серию опытов с маятником новой длины и вычислите его период колебаний по формуле 
.
9. Вычислите частоты колебаний для обеих маятников по формулам 
и 
.
10. Сравните периоды колебаний двух маятников, длины которых отличались в четыре раза, и сделайте вывод относительно справедливости формулы (1). Укажите возможные причины расхождения результатов.
11. Ответьте на контрольные вопросы.
Контрольные вопросы
1. Что называют периодом колебаний маятника?
2. Что называют частотой колебаний маятника? Какова единица частоты колебаний?
3. От каких величин и как зависит период колебаний математического маятника?
4. От каких величин и как зависит период колебаний пружинного маятника?
5. Какие колебания называют собственными?
Лабораторная работа № 4.
Тема: Изучение зависимости периода колебаний нитяного маятника от длины нити.
Оборудование: штатив с перекладиной и муфтой, нить с петлями на концах, груз с крючком, линейка, электронный секундомер
Цель работы: состоит в экспериментальной проверке формулы, связывающей период колебаний маятника с длиной его подвеса.
Основные сведения
Рассмотрим колебания нитяного маятника, т.е. небольшого тела (например, шарика), подвешенного на нити, длина которой значительно превышает размеры самого тела. Если шарик отклонить от положения равновесия и отпустить, то он начнет колебаться. Сначала маятник движется с нарастающей скоростью вниз. В положении равновесия скорость шарика не равна нулю, и он по инерции движется вверх. По достижении наивысшего положения шарик снова начинает двигаться вниз. Это будут свободные колебания маятника.
Свободные колебания – это колебания, которые возникают в системе под действием внутренних сил, после того, как система была выведена из положения устойчивого равновесия.
Колебательное движение характеризуют амплитудой, периодом и частотой колебаний.
Амплитуда колебаний - это наибольшее смещение колеблющегося тела от положения равновесия. Обозначается А. Единица измерения - метр [1м].
Период колебаний - это время, за которое тело совершает одно полное колебание. Обозначается Т. Единица измерения - секунда [1с].
Частота колебаний - это число колебаний, совершаемых за единицу времени. Обозначается ν. Единица измерения - герц [1Гц].
Тело, подвешенное на невесомой нерастяжимой нити называют математическим маятником.
Период колебаний математического маятника определяется формулой: 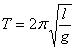(1), где l – длина подвеса, а g – ускорение свободного падения.
Период колебаний математического маятника зависит:
1) от длины нити. Период колебаний математического маятника пропорционален корню квадратному из длины нити . Т.е., например при уменьшении длины нити в 4 раза, период уменьшается в 2 раза; при уменьшении длины нити в 9 раз, период уменьшается в 3 раза.
2) от ускорения свободного падения той местности, где происходят колебания. Период колебаний математического маятника обратнопропорционален корню квадратному из ускорения свободного падения .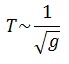
Тело, подвешенное на пружине называют пружинным маятником.
Период колебаний пружинного маятника определяется формулой 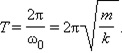где m - масса тела, k - жесткость пружины.
Период колебаний пружинного маятника зависит:
1) от массы тела. Период колебаний пружинного маятника пропорционален корню квадратному из массы тела .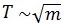
2) от жесткости пружины. Период колебаний пружинного маятника обратнопропорционален корню квадратному из жесткости пружины.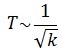
В работе мы исследуем колебания математического маятника. Из формулы 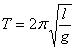следует, что период колебаний изменится вдвое при изменении длины подвеса в четыре раза.
Это следствие и проверяют в работе. Поочередно испытывают два маятника, длины подвесов которых отличаются в четыре раза. Каждый из маятников приводят в движение и измеряют время, за которое он совершит определённое количество колебаний. Чтобы уменьшить влияние побочных факторов, опыт с каждым маятником проводят несколько раз и находят среднее значение времени, затраченное маятником на совершение заданного числа колебаний. Затем вычисляют периоды маятников и находят их отношение.
Выполнение работы.
1. Подготовьте таблицу для записи результатов измерений и вычислений:
|
l, м |
№ опыта |
N |
t, с |
tср, с |
Т, с |
ν, Гц |
|
l1 = |
1 |
30 |
|
|
|
|
|
2 |
30 |
|
||||
|
3 |
30 |
|
||||
|
4 |
30 |
|
||||
|
l2 = |
1 |
30 |
|
|
|
|
|
2 |
30 |
|
||||
|
3 |
30 |
|
||||
|
4 |
30 |
|
2. Закрепите перекладину в муфте у верхнего края стержня штатива. Штатив разместите на столе так, чтобы конец перекладины выступал за край поверхности стола. Подвесьте к перекладине с помощью нити один груз из набора. Расстояние от точки повеса до центра груза должно быть 25-30 см.
3. Подготовьте электронный секундомер к работе в ручном режиме.
4. Отклоните груз на 5-6 см от положения равновесия и замерьте время, за которое груз совершит 30 полных колебаний (при отклонении груза следите, чтобы угол отклонения не был велик).
5. Повторите измерение 3-4 раза и определите среднее время tср1=(t1+t2+t3+t4)/4
6. Вычислите период колебания груза с длиной подвеса 25-30 см по формуле .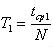
7. Увеличьте длину подвеса в четыре раза.
8. Повторите серию опытов с маятником новой длины и вычислите его период колебаний по формуле .
9. Вычислите частоты колебаний для обеих маятников по формулам и .
10. Сравните периоды колебаний двух маятников, длины которых отличались в четыре раза, и сделайте вывод относительно справедливости формулы (1). Укажите возможные причины расхождения результатов.
11. Ответьте на контрольные вопросы.
Контрольные вопросы
1. Что называют периодом колебаний маятника?
2. Что называют частотой колебаний маятника? Какова единица частоты колебаний?
3. От каких величин и как зависит период колебаний математического маятника?
4. От каких величин и как зависит период колебаний пружинного маятника?
5. Какие колебания называют собственными?
Вариант выполнения лабораторной работы.
Результаты измерений:
|
l, м |
№ опыта |
N |
t, с |
tср, с |
Т, с |
ν, Гц |
|
l1 = |
1 |
30 |
29 |
|
|
|
|
2 |
30 |
28 |
||||
|
3 |
30 |
28 |
||||
|
4 |
30 |
29 |
||||
|
l2 = |
1 |
30 |
53 |
|
|
|
|
2 |
30 |
54 |
||||
|
3 |
30 |
54 |
||||
|
4 |
30 |
54 |
Звук - это упругие продольные волны частотой от 20 Гц до 20000 Гц, вызывающие у человека слуховые ощущения.
Источник звука - различные колеблющиеся тела, например туго натянутая струна или тонкая стальная пластина, зажатая с одной стороны.
Как возникают колебательные движения? Достаточно оттянуть и отпустить струну музыкального инструмента или стальную пластину, зажатую одним концом в тисках, как они будут издавать звук. Колебания струны или металлической пластинки передаются окружающему воздуху. Когда пластинка отклонится, например в правую сторону, она уплотняет (сжимает) слои воздуха, прилегающие к ней справа; при этом слой воздуха, прилегающий к пластине с левой стороны, разредится. При отклонении пластины в левую сторону она сжимает слои воздуха слева и разрежает слои воздуха, прилегающие к ней с правой стороны, и т.д. Сжатие и разрежение прилегающих к пластине слоев воздуха будет передаваться соседним слоям. Этот процесс будет периодически повторяться, постепенно ослабевая, до полного прекращения колебаний .
Таким образом колебания струны или пластинки возбуждают колебания окружающего воздуха и, распространяясь, достигают уха человека, заставляя колебаться его барабанную перепонку, вызывая раздражение слухового нерва, воспринимаемое нами как звук.
Скорость распространения звуковых волн в разных средах неодинакова. Она зависит от упругости среды, в которой они распространяются. Медленнее всего звук распространяется в газах. В воздухе скорость распространения звуковых колебаний в среднем равна 330 м/с, однако она может изменяться в зависимости от его влажности, давления и температуры. В безвоздушном пространстве звук не распространяется. В жидкостях звук распространяется быстрее. В твердых телах – еще быстрее. В стальном рельсе, например, звук распространяется со скоростью » 5000 м/с.
При распространении звука в атомы и молекулы колеблются вдоль направления распространения волны, значит звук - продольная волна.
ХАРАКТЕРИСТИКИ ЗВУКА
1. Громкость. Громкость зависит от амплитуды колебаний в звуковой волне. Громкость звука определяется амплитудой волны.
За единицу громкости звука принят 1 Бел (в честь Александра Грэхема Белла, изобретателя телефона). Громкость звука равна 1 Б, если его мощность в 10 раз больше порога слышимости.
На практике громкость измеряют в децибелах (дБ).
1 дБ = 0,1Б. 10 дБ – шепот; 20–30 дБ – норма шума в жилых помещениях;
50 дБ – разговор средней громкости;
70 дБ – шум пишущей машинки;
80 дБ – шум работающего двигателя грузового автомобиля;
120 дБ – шум работающего трактора на расстоянии 1 м
130 дБ – порог болевого ощущения.
Звук громкостью свыше 180 дБ может даже вызвать разрыв барабанной перепонки.
2. Высота тона. Высота звука определяется частотой волны, или частотой колебаний источника звука.
Звуки человеческого голоса по высоте делят на несколько диапазонов:
- бас – 80–350 Гц,
- баритон – 110–149 Гц,
- тенор – 130–520 Гц,
- дискант – 260–1000 Гц,
- сопрано – 260–1050 Гц,
- колоратурное сопрано – до 1400 Гц.
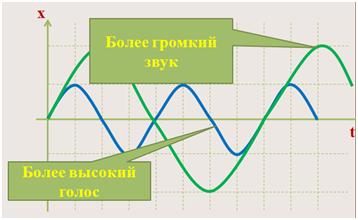
Человеческое ухо способно воспринимать упругие волны с частотой примерно от 16 Гц до 20 кГц. А как мы слыщим?
Слуховой анализатор человека - ухо - состоит их четырех частей:
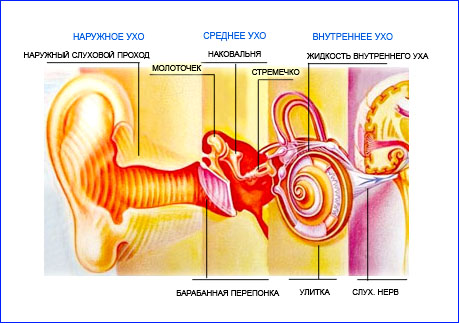
Наружное ухо
К наружному уху относятся ушная раковина, слуховой проход и барабанная перепонка, которая закрывает внутренний конец слухового прохода. Слуховой проход имеет неправильную изогнутую форму. У взрослого человека длина его составляет около 2,5 см, а диаметр около 8 мм. Поверхность слухового прохода покрыта волосками и содержит железы, выделяющие ушную серу, которая необходима для поддержания влажности кожи. Слуховой проход обеспечивает также постоянную температуру и влажность барабанной перепонки.
Среднее ухо
Среднее ухо – это заполненная воздухом полость за барабанной перепонкой. Эта полость соединяется с носоглоткой посредством евстахиевой трубы – узкого хрящевого канала, который обычно находится в закрытом состоянии. Глотательные движения открывают евстахиеву трубу, что обеспечивает поступление воздуха в полость и выравнивание давления по обе стороны барабанной перепонки для ее оптимальной подвижности. В полости среднего уха находятся три миниатюрные слуховые косточки: молоточек, наковальня и стремя. Одним концом молоточек соединен с барабанной перепонкой, другой его конец связан с наковальней, которая, в свою очередь соединена со стременем, а стремя с улиткой внутреннего уха. Барабанная перепонка постоянно колеблется под действием улавливаемых ухом звуков, а слуховые косточки передают ее колебания во внутреннее ухо.
Внутреннее ухо
Во внутреннем ухе содержится несколько структур, но к слуху отношение имеет только улитка, получившая свое название из-за спиральной формы. Улитка разделена на три канала, заполненные лимфатическими жидкостями. Жидкость в среднем канале отличается по составу от жидкости в двух других каналах. Орган, непосредственно ответственный за слух (Кортиев орган), находится в среднем канале. Кортиев орган содержит около 30000 волосковых клеток, которые улавливают колебания жидкости в канале, вызванные движением стремени, и генерируют электрические импульсы, которые по слуховому нерву передаются к слуховой зоне коры головного мозга. Каждая волосковая клетка реагирует на определенную звуковую частоту, причем высокие частоты улавливаются клетками нижней части улитки, а клетки, настроенные на низкие частоты, располагаются в верхней части улитки. Если волосковые клетки по каким-либо причинам гибнут, человек перестает воспринимать звуки соответствующих частот.
Слуховые проводящие пути
Слуховые проводящие пути – это совокупность нервных волокон, проводящих нервные импульсы от улитки к слуховым центрам коры головного мозга, в результате чего возникает слуховое ощущение. Слуховые центры расположены в височных долях головного мозга. Время, потраченное на прохождение слухового сигнала от внешнего уха к слуховым центрам мозга, составляет около 10 миллисекунд.
Восприятие звука
Ухо последовательно преобразует звуки в механические колебания барабанной перепонки и слуховых косточек, затем в колебания жидкости в улитке и, наконец, в электрические импульсы, которые по проводящим путям центральной слуховой системы передаются в височные доли мозга для распознавания и обработки.
Мозг и промежуточные узлы слуховых проводящих путей извлекают не только информацию о высоте и громкости звука, но и другие характеристики звука, например, интервал времени между моментами улавливания звука правым и левым ухом – на этом основана способность человека определять направление, по которому приходит звук. При этом мозг оценивает как информацию, полученную от каждого уха в отдельности, так и объединяет всю полученную информацию в единое ощущение.
В нашем мозгу хранятся «шаблоны» окружающих нас звуков – знакомых голосов, музыки, опасных звуков и т.д. Это помогает мозгу в процессе обработки информации о звуке быстрее отличить знакомые звуки от незнакомых. При снижении слуха мозг начинает получать искаженную информацию (звуки становятся более тихими), что приводит к ошибкам в интерпретации звуков. С другой стороны, нарушения в работе мозга в результате старения, травмы головы или неврологических болезней и расстройств могут сопровождаться симптомами, похожими на симптомы снижения слуха, например, невнимательность, отрешенность от окружения, неадекватная реакция. Для того чтобы правильно слышать и понимать звуки, необходима согласованная работа слухового анализатора и мозга. Таким образом, без преувеличения можно сказать, что человек слышит не ушами, а мозгом!
Животные в качестве звука воспринимают волны иных частот.
Ультразвук - продольные волны с частотой превышающей 20 000Гц.
Применение ультразвука.
С помощью гидролокаторов установленных на кораблях измеряют глубину моря, обнаруживают косяки рыб, встречный айсберг или подводную лодку.
Ультразвук используют в промышленности для обнаружения дефектов в изделиях.
В медицине при помощи ультразвука осуществляют сварку костей, обнаруживают опухоли, осуществляют диагностику заболеваний.
Биологическое действие ультразвука позволяет использовать его для стерилизации молока, лекарственных веществ, а также медицинских инструментов.
Совершенные ультразвуковые локаторы имеют летучие мыши и дельфины.
Видео по теме "Звуковые волны":
Источники звука Звуковые волны